If you told me six months ago that I would be here on the web arguing the merits of statistical analysis to prove or disprove a theory I would have laughed out loud at you. However, about 3 months ago I began training where I work to become skilled in the art of studying variance. As some may be aware, Motorola started a program back in the early 1980s to study variances in manufacturing processes, and make predictions based on that study. Their in house effort has bloomed in the last 20 years to a very robust program called "Six Sigma".

Six Sigma is a very rigorous program by which a process is studied by gathering data representative of the process and analyzing it to see what it tells you. Once you analyze it, you draw conclusions and can even make predictions about future behavior. It is not my attempt on this page to provide an in depth education on statistical analysis, but rather to look at Eric von Sneidern's study of Disston blade composition and hardness, and to see if the conclusion that is drawn is supported by the data.

Eric's study which you can read here looks at five different handsaws, each a different model in the Disston line, and analyzes the steel composition and blade hardness for each saw. The study attempts to confirm or deny that there is a real difference in the steel comprising the various handsaw models. Some believe that the differences are merely a marketing tactic to increase sales in one way or another and that no real difference exists.

I heartily commend Eric for the time and effort he spent in conducting the analysis. It is a first of a kind work in this area. I first speculated in the Summer of 1998 in an article that I wrote for the Fine Tool Journal about the relative grades of steel and that a thorough analysis would need to be done to substantiate the Disston claim that one hand saw was better than another based on the steel used.

Unfortunately, the conclusion that Eric draws in his study that the steel types aren't different simply can't be supported by the data that he provides. Further, the way the study was conducted is flawed in several ways, first with respect to the sample size that was used for the study, and second that different vintages of saws were used in the study. In the text and graphs that follow, I will explain how I came to this conclusion. Hold on, the ride is about to get bumpy.

The study of manufacturing outputs has been going on for many years. In any process, there is a distribution of values that comprise any population. For instance, for the sake of this example, lets say that Disston could make 1000 D12 handsaws a week. Each week they mixed up and used a different melt of steel. Further, once the steel was rolled and punch, the steel was tempered in batches of 50 in an oven. Let's say that they did this every week for a year. At the end of the year, they would have made about 50,000 saws. That population would be comprised of 50 different melts of steel, and 1000 different tempering batches. Then, let's say that all the saws were sold to the public. And Disston repeated this every year for 20 years. Now, let's say that you went across the country and bought 1000 of the 1,000,000 handsaws and tested each one to determine the range of hardness in the population. Naturally, in any process there is variation. We want to know how much. A graph of that distribution might look like the chart below:

For all the graphs in this treatise, I used version 13.0 of Minitab, a statistical analysis tool which can generate random samples of data. I created two sets of populations. One was for D12 saws and one for D8. I told the random sample generator to make random samples for each saw type with populations of 3, 10 and 1000. For each population, the standard deviation was 1.0. For the D12 samples, the average, or the mean, was set to 55. For the D8 samples, the mean was set to 53. I reasoned that if I was Disston, those would be good values to have corresponding to the relative quality of the saw and would represent hardnesses on the Rockwell C Scale of 53 and 55.

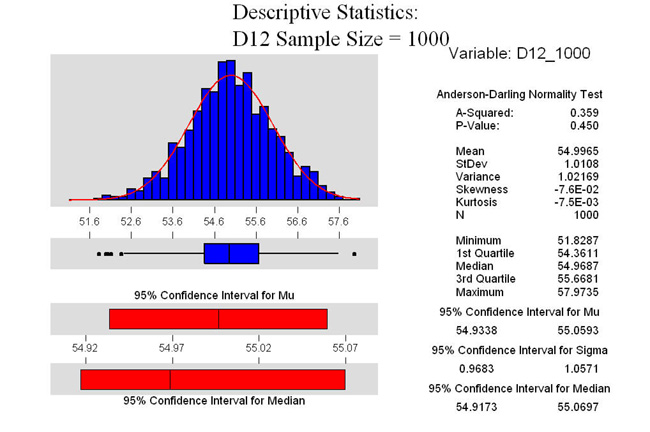
In the example at the right, we can see that the data is normally distributed. A normal distribution is often characterized by a bell shaped curve. The graph at the right is called a histogram. As we can see from the descriptive statistics, the mean is calculated at 54.9965 and the standard deviation is 1.0108. They are not exactly 55 and 1 because of the random number generator that Minitab used to generate the sample. There are two other important numbers on this graph.

One is P which we can see is .450. In statistics, there is what is known as the null hypothesis. The null hypothesis says (depending on what test you are looking at) that unless you can prove otherwise, there is no difference between two measurements. The alternate hypothesis says that there is a difference. P is a measure of how confident you are in making a choice between the two. In statistics, it is usually agreed that a 5% risk is all that you are willing to take with respect to these two tests. Here, we see that P is .450. For this Normality test, that means that if you reject the null hypothesis, the risk of you being wrong is 45%. Boiled down in practical terms, if P is greater than .05 (in this example), we can say that the data is normal. If it were less than .05, we would draw the conclusion that the data is not normally distributed. This determination is important because the tests that we will use later on are based on the assumption that the data is normal. Of course, I know that it is normal because I used the normal random number generator to make up the sample.

The other part of this graph that is important is the Confidence Interval for the Mean (or Mu). In the graph above, we see that the 95% confidence interval is between 54.9338 and 55.0593. That means, that for this population, we are 95% confident that the true mean of the total population is somewhere between those two numbers. Remember, we are only testing 1000 of the 1,000,000 saws that exist. If we measured them all, we would know the exact mean, known as X bar. Since we are only looking at a representative sample of the total population, we don't know exactly what the real mean is. However, if we took 10 samples out of the thousand, measured the mean, and then put them back, and did this over and over and over again, we would get what we call a standard distribution of the mean. The bigger the sample and the more times we do the random sampling of 10, the more confident we are of the result. This is a very important point that we will look at as we go forward.

OK, now that I've thoroughly bored you with some statistical theory, lets continue on our example. The graphs below compare the normally distributed populations of the D8 sample and the D12 sample. In the two graphs that follow, the size of the sample is 1000. Remember, I told the random number generator to give me average hardness values of 53 and 55 for the D8 and D12 saws respectively.

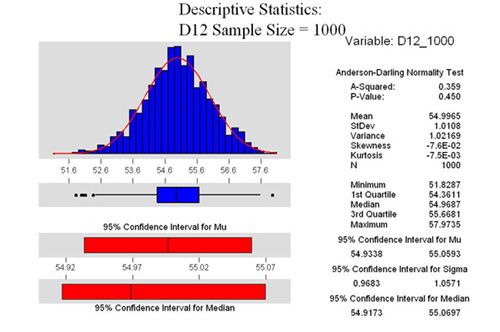
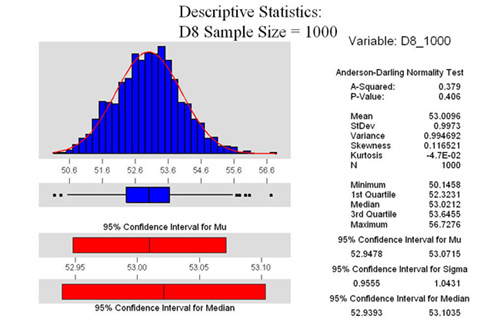From the two graphs at the right, we see that both are Normally Distributed. Further, we see that the 95% confidence interval for the mean for the D8 sample is between 52.9478 and 53.0715. Quite a narrow range. For the D12 sample, we see that it is between 54.9338 and 55.0593.

Of course, statistically, we are interested if those two means are different enough to say with confidence that they are indeed different. To prove that, first we have to do what is called an F test which tests for equal variance in the sample. I ran it for all the samples, and it said that the variances in the two samples were equal. I won't go into the test, just trust me when I tell you they are. This assumption is important to do the next test, a 2 sample T test.

Just this one last test, and we can look at some graphs for different sample sizes which will illustrate my point. There is a point to this, just hang in there a little longer.

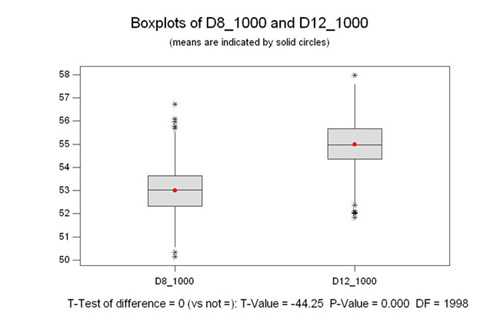
At the right we are comparing the two populations above. This type of graph is called a box plot. The box represents 50% of the population, and the whiskers show the upper and lower 25% of the population. The asterisks are outliers, that is data which is outside the expected normal distribution. The line in the box is the median for the population. The median is the middle value, meaning that there are as many values above it as below it. It is different than the mean, or the average. The mean is the red dot.

Ok, on to the T test. The whole point of the T test is to prove if the means are different or not. The bottom line of the graph shows that the P value is 0.000. That means that we have to reject the null hypothesis and accept the alternate hypothesis. Put another way, there is 0% chance of being wrong is you say the means are different. I'm sure you are saying, "Duh, no kidding, any fool can see that". True, but stick with me, it's about to get interesting.

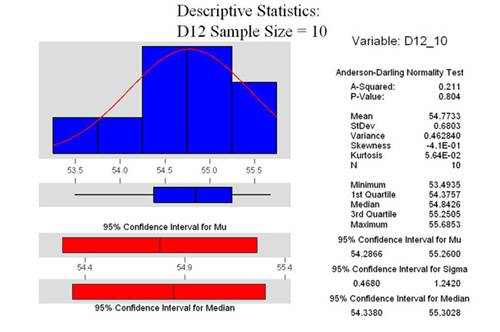
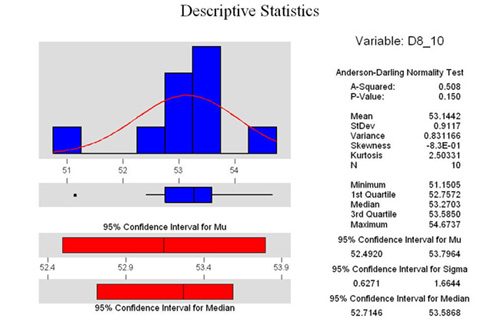At the right are the same three graphs, only using a sample size of 10. As we can see from the P values all the data is normally distributed, although the D12 sample is a lot more normal than the D8 sample. Both are within the parameters of the test however.

I would like to draw your attention to the confidence interval of the mean for each graph. Notice how it has widened out when we only look at 10 samples.

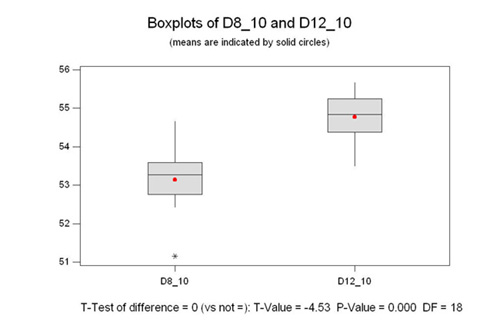
Look at the 2 sample T test, we see however, that there is still a 0% chance of being wrong if we say that the means are different.

OK, I'm sure you are saying , so what...where is this going. One last example.

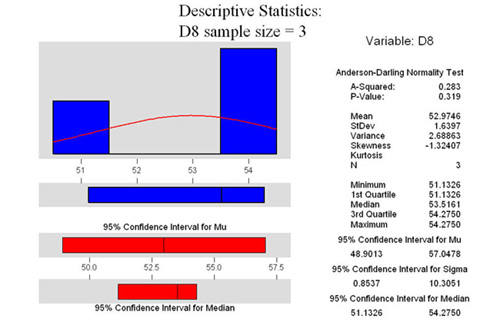OK, look at the three graphs at the right. Remember, they were randomly generated using the same parameters as above. I just told the computer to only make three samples instead of 10 or 1000. Notice that both are normal (from P>.05). But look at the 95% confidence interval of the mean. From roughly 50 to 57 for the D8, and from 52 to 56.7 for the D12. Remember that means that we are 95% confident that the true mean is somewhere in that range. Notice how they are almost the same range?

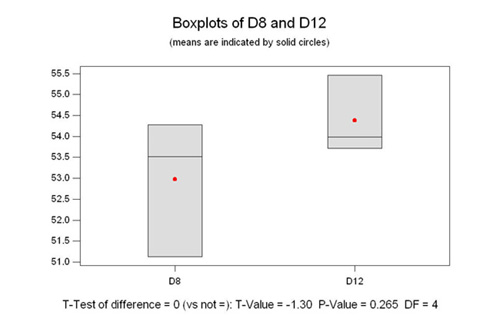
Looking at the 2 sample T analysis, we see that the P value is .265. That means that if we say that the means are different, we run a 27% risk of being wrong. Therefore, in this case we have to accept the null hypothesis which says that they are in fact statistically the same.

Ta Da! There is the punch line. I couldn't run the test for a sample size of less than 3, but, you get the idea. Further, look at the boxplot in the 2 sample T test. See how they overlap? This is the most important point in this long essay.

When you have a small sample size, you can't tell with any confidence if you picked a sample that is truly representative of entire population, or you picked one that was way out on the edge of the bell shaped curve. The closer two populations are together, the more their distributions overlap. To tell the difference you need a very large sample size. Thousands or tens of thousands. Conversely, if the means of two populations are very far apart, you can have a very small sample size and still be able to distinguish between the two.

Well, if you suffered through all that without nodding off, you must be really interested in this stuff, so I owe it to you to tie it all together. As I've just demonstrated, you can't possibly sample just one saw out of a population of millions and draw any conclusion from it. To do a proper study that you could believe in, you would have to do the following. Find a sample of at least 30 saws of each type, and have each type be in the same age range as the others. For instance, you would not want to test a 1950s vintage D23, and an 1890 vintage #7. You would want to test all the saws from the same age range. What you are trying to do is take all the variation out of the sample that you can, so other variables can't influence your test. 30 is a good sample size to use for any study like this as it is a good compromise. Ideally we would want to test them all to get the real mean (X bar as it is known), instead of Mu, which is the mean of a representative sample.

I used hardness in this example because the numbers were easy to work with. The exact same theory applies to any of the other things measured...nickel or carbon content, etc. In fact, in Eric's test, he comments how the back saw is much harder than most, as evidenced by the fragile teeth. This saw is very far away from the real mean of hardness....out at the thin edge of the bell shaped curve (maybe even six standard deviations away). If you only tested this saw, and didn't know anything about steel or hardness, you might conclude that all back saws were this hard. We know that isn't the case. This one example points out the severe flaw in this study.

I realize that I don't know what Disston intended for the actual hardness of a D8 and a D12. I also don't know if the standard deviation is 1, 2 or maybe .5. This is important as it affects how far apart the populations have to be to tell the difference between them. A standard deviation of 2 has a curve that is much wider than the same curve with a standard deviation of one. For the sake of the example, I kept the Standard Deviation the same. I am willing to bet that populations are normally distributed. If they aren't, we could use other tests on the median which would tell us the same thing.

In summary, I hope that no one thinks that I am throwing stones at the effort that Eric put out to do what he did. Having said that, you just can't draw any conclusion from his efforts except that for the 5 saws he tested, the results are as he posted them on his site. You simply can't extrapolate what you see for one saw and say that it is the same as all saws of that particular type. It just doesn't work.

Yours in Statistical Analysis,

Pete Taran, Six Sigma Black Belt in training (who also knows a lot about saws)